Question

Use the Law of Sines to find the missing angle of the triangle

find mB to the nearest tenth

155.4°
24.6°
65.7°
76.3°

Answer 1

`m\angle B=76.3^(\circ)`

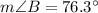
Explanation:

For any triangle, the Law of Sines is given by
`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`.

Using this, we can set up the following equation:

`(\sin 38^(\circ))/(50)=(\sin C)/(74)`

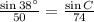
Solving, we get:

`\sin C=(74\sin 38^(\circ))/(50)=0.91117898348,\\C=\arcsin(0.91117898348)=65.66879`

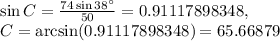
Since there are 180 degrees in a triangle:

`m\angle B+38+65.66879=180, \\m\angle B\approx \boxed{76.3^(\circ)}`

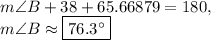
*It is worth noting that there is more than one possible answer for the measure of angle B. Since
`\sin\theta=\sin(180-\theta)`, there may be up to two answers when using the Law of Sines to solve for an angle. In this case, there are two possible triangles given the information given, however, only one option is given in the answer choices.