Answer:
- L < 1, so by series ratio test, It is convergent
- sum of the convergent series is 49
Explanation:
Given the data in the question;
series = 7 + 6 + 36/7 + 216/49 + .........
⇒ 7 + 7 × 6/7 + 7 × 36/49 + 7 × 216/343 +........
⇒ 7 + 7 × 6/7 + 7 × 6²/7² + 7 × 6³/7³ .....
⇒ 7( 1 + 6/7 + 6²/7² + 6³/7³ + ..... )
⇒ 7 ∞∑_

 6/7
6/7
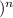
⇒ ∞∑_
 (
(
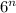 /
/
 )
)
So, L =

=
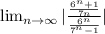
=

= 6 /7
L < 1
so by series ratio test,
It is convergent
So we find the sun;
Sum of infinite geometric series is;
⇒ a / (1-r)
here, a = first number and r = common ratio
∑ = 7( 1 + 6/7 + 6²/7² + 6³/7³ + ..... )
a = 1 and r = 6/7
so
∑ = 7(
 )
)
= 7(
 )
)
= 7(
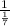 )
)
= 7( 7 )
= 49
Therefore, sum of the convergent series is 49