Question

Building A is 490 feet tall and Building B is 754 feet tall. If the angle of depression from the top of Building B to the top of Building A is 46°, how far apart are the buildings?

Answer 1

Answer:
`254.94\ ft`

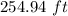
Explanation:

Given

Building A is 490 feet tall and building B is 754 ft tall.

If the angle of depression from building B to the top of building A is
`46^(\circ)`

Difference in the height of the two buildings is
`754-490=264\ ft`

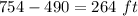
If the difference between them is
`x`

From the figure, we can write

`\Rightarrow \tan 46^(\circ)=(264)/(x)\\\\\Rightarrow x=(264)/(\tan 46^(\circ))\\\\\Rightarrow x=254.94\ ft`

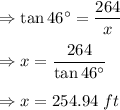
Therefore, the two buildings are
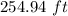`254.94\ ft` apart.