Question

For a data set of the pulse rates for a sample of adult? females, the lowest pulse rate is 39 beats per? minute, the mean of the listed pulse rates is x overbarxequals=74.0 beats per? minute, and their standard deviation is sequals=11.4 beats per minute.

a. What is the difference between the pulse rate of 39 beats per minute and the mean pulse rate of the? females?
b. How many standard deviations is that? [the difference found in part? (a)?
c. Convert the pulse rate of 39 beats per minutes to a z score.

Answer 1

a) The difference is of 35 beats per minute.

b) So 3.07 standard deviations below the mean.

c) Z = -3.07.

Explanation:

Z-score:

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

In this question:

Mean
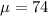`\mu = 74`, standard deviation
`\sigma = 11.4`

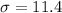
a. What is the difference between the pulse rate of 39 beats per minute and the mean pulse rate of the? females?

39 - 74 = -35

The difference is of 35 beats per minute.

b. How many standard deviations is that? [the difference found in part? (a)?

|Z| when X = 39. So

`Z = (X - \mu)/(\sigma)`

`Z = (39 - 74)/(11.4)`

`Z = -3.07`

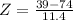
|Z| = 3.07

So 3.07 standard deviations below the mean.

c. Convert the pulse rate of 39 beats per minutes to a z score.

From item b. above, Z = -3.07.