Answer:
a) The linear function that models the volume of hydrogen in the balloon at any time
 is
is
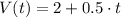 .
.
b) 26 seconds are needed to completely fill the balloon.
Explanation:
The statement has a mistake, the correct form is described below:
Weather balloons are filled with hydrogen and released at various sites to measure and transmit data about conditions such as air pressure and temperature. A weather balloon is filled with hydrogen at the rate of
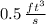 . Initially, the balloon has
. Initially, the balloon has
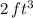 of hydrogen.
of hydrogen.
a) The volume of weather balloons is increasing linearly in time (
 ), in seconds, since the rate of change of volume (
), in seconds, since the rate of change of volume (
 ), in cubic feet per second, is stable. The linear function of the volume of the weather balloon in terms of time is:
), in cubic feet per second, is stable. The linear function of the volume of the weather balloon in terms of time is:
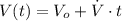 (1)
(1)
Where:
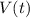 - Current volume, in cubic feet.
- Current volume, in cubic feet.
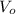 - Initial volume, in cubic feet.
- Initial volume, in cubic feet.
If we know that
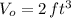 and
and
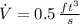 , then the volume as a function of time is:
, then the volume as a function of time is:
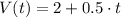
b) If we know that
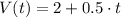 and
and
 , then the time taken to fill the balloon is:
, then the time taken to fill the balloon is:
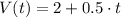
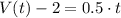

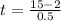
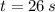
26 seconds are needed to completely fill the balloon.