Question

Find the mean absolute deviation of the set of data. Round your answer to two decimal places. 21.3, 11.5, 51.6, 35, 18.8, 49

Answer 1

Answer: 14

Explanation:

The mean absolute deviation of a dataset is defined as the average distance between each datav alue and the mean.

It is computed by formula:

`(1)/(n)\sum^n_(i=1)|x_i-\overline{x}|`

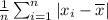
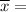`\overline{x}=`average value of the data set

n = number of data values

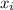`x_i` = data values in the set

`\overline{x}=(21.3+11.5+51.6+35+18.8+49)/(6)\\\\=31.2`

MAD=
`(|21.3-31.2|+|11.5-31.2|+|51.6-31.2|+|35-31.2|+|18.8-31.2|+|49-31.2|)/(6)`

=
`(9.9+19.7+20.4+3.8+12.4+17.8)/(6)`

=14

Hence, the mean absolute deviation of the set of data = 14