Question

A friend of mine is giving a dinner party. His current wine supply includes 9 bottles of zinfandel, 10 of merlot, and 12 of cabernet, all from different wineries. He will serve five bottles of the wines during dinner in a particular order,

(a) How many distinct sequences are there of serving any five wines?
(b) If the first two wines have to be zinfandel and the last three must either be merlot or cabernet, how many ways can this be done?
(c) If the wine sequence is formed randomly, what is the probability that none of the wines served is a zinfandel?

Answer 1

Explanation:

From the given information:

The total number of wine = 9 + 10 + 12 = 31

(1)

The number of distinct sequences used for serving any five wines can be estimated by using the permutation of the number of total wines with the number of wines served.

i.e

=
`^(31)P_5`

`=(31!)/((31-5)!)`

`=(31!)/((26)!)`

`=(31* 30* 29* 28* 27* 26!)/((26)!)`

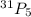
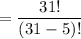
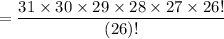
= 20389320

(2)

If the first two wines served = zinfandel and the last three is either merlot or cabernet;

Then, the no of ways we can achieve this is:

=
`^9P_2* ^(22)P_3`

`= (9!)/((9-2)!)* (22!)/((22-3)!)`

`= (9!)/((7)!)* (22!)/((19)!)`

`= (9*8*7!)/((7)!)* (22*21*20*19!)/((19)!)`

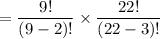
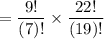
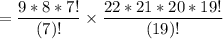
= 665280

(3)

The probability that no zinfandel is served is computed as follows:

Total wines (with zinfandel exclusion) = 31 - 9 = 22

Now;

the required probability is:

`= (^(22)P_5 )/(^(31)P_5)`

`= \frac{(22!)/((22-5)!) } {(31!)/((31-5)!) }`

`= \frac{(22!)/(17!) } {(31!)/((26)! )}`

`= \frac{((22*21*20*19*18*17!)/(17!))} {((31*30*29*28*27*26!)/((26)! ))}`

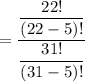
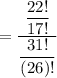
= 0.1549

≅ 0.155