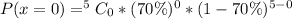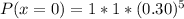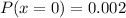Answer:
 ---- At least 5 from marketing departments are extroverts
---- At least 5 from marketing departments are extroverts
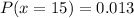 ---- All from marketing departments are extroverts
---- All from marketing departments are extroverts
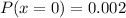 ---------- None from computer programmers are introverts
---------- None from computer programmers are introverts
Explanation:
See comment for complete question
The question is an illustration of binomial probability where

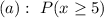
 --- marketing personnel
--- marketing personnel
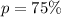 --- proportion that are extroverts
--- proportion that are extroverts
Using the complement rule, we have:
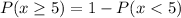
So, we have:
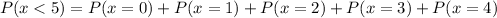
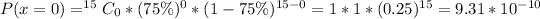
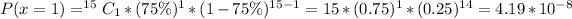
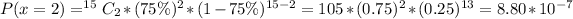
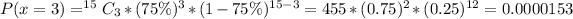

So, we have:


Recall that:
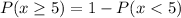
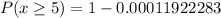
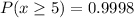
 --- approximated
--- approximated

 --- marketing personnel
--- marketing personnel
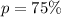 --- proportion that are extroverts
--- proportion that are extroverts
So, we have:

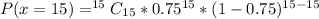
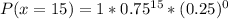
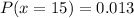
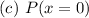
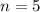 ---------- computer programmers
---------- computer programmers
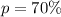 --- proportion that are introverts
--- proportion that are introverts
So, we have: