Question

Mrs. Giavis has 26 marbles in a bag. She has 13 blue marbles, 10 red marbles, and 3 yellow marbles. What is the probably that Mrs. Giavis will pick a blue marble, not replace it, and then randomly pick a red marble?

Answer 1

Given:

Total number of marbles = 26

Number of blue marbles = 13

Number of red marbles = 10

Number of yellow marbles = 3

To find:

The probability of getting a blue marble then a red marble (without replacement).

Solution:

Total number of marbles = 26

Number of blue marbles = 13

Probability of getting a blue marble is first draw is:

`P(Blue)=\frac{\text{Number of blue marbles}}{\text{Total number of marbles}}`

`P(Blue)=(13)/(26)`

`P(Blue)=(1)/(2)`

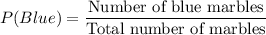
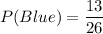
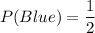
After drawing 1 marble, the remaining number of marbles in the bag is 25.

Probability of getting a red marble is second draw is:

`P(Red)=\frac{\text{Number of red marbles}}{\text{Remaining number of marbles}}`

`P(Red)=(10)/(25)`

`P(Red)=(2)/(5)`

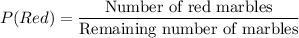
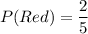
Now the probability of getting a blue marble then a red marble (without replacement) is:

`P(\text{Blue then red})=P(Blue)* P(Red)`

`P(\text{Blue then red})=(1)/(2)* (2)/(5)`

`P(\text{Blue then red})=(1)/(5)`

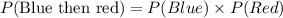
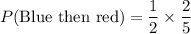
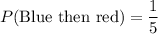
Therefore, the probability of getting a blue marble then a red marble (without replacement) is
`(1)/(5)`.