Selecting two marbles from a bag containing the numbers 2,4,6,8,10,12 (with replacement) what is the probability of selecting two numbers less than 10 ?

Question

asked Sep 25, 2022 203k views

1 Answer

Qadir · Answer 1 · 2022-09-30T15:18:36+0000

Given:

A bag containing the numbers 2,4,6,8,10,12.

To find:

The probability of selecting two numbers less than 10.

Solution:

We have,

Total numbers = 6

Numbers less than 10 are 2,4,6,8.

Numbers less than 10 = 4

Probability of getting a number less than 10 is:

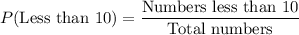
$P(\text{Less than 10})=\frac{\text{Numbers less than 10}}{\text{Total numbers}}$

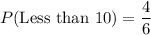
$P(\text{Less than 10})=(4)/(6)$

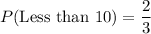
$P(\text{Less than 10})=(2)/(3)$

We select the second number with replacement. So, the probability of second draw is same as the probability for first draw.

Probability of selecting two numbers less than 10 is:

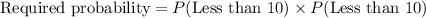
$\text{Required probability}=P(\text{Less than 10})* P(\text{Less than 10})$

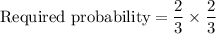
$\text{Required probability}=(2)/(3)* (2)/(3)$

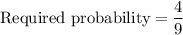
$\text{Required probability}=(4)/(9)$

Therefore, the probability of selecting two numbers less than 10 is
.