Answer:
m₀ = 96 g
Step-by-step explanation:
First, we will calculate the no. of half-lives passed:
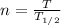
where,
n = no. of half-lives passed = ?
T = Total time elapsed = 32 h
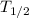 = Half-Life = 8 h
= Half-Life = 8 h
Therefore,
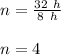
Now, for the initial amount of element:
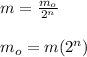
where,
m₀ = initial amount of element = ?
m = current amount of element = 6 g
Therefore,
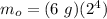
m₀ = (6 g)(16)
m₀ = 96 g