Question

Suppose that the middle 68% of speeding ticket fines on a highway fall between 93.18 and 118. Give an approximate estimate of the standard deviation of the speeding ticket fines. Assume the fine amount has a normal distribution

Answer 1

The approximate estimate of the standard deviation of the speeding ticket fines is of 12.41.

Explanation:

The Empirical Rule states that, for a normally distributed random variable:

Approximately 68% of the measures are within 1 standard deviation of the mean.

Approximately 95% of the measures are within 2 standard deviations of the mean.

Approximately 99.7% of the measures are within 3 standard deviations of the mean.

Middle 68% of speeding ticket fines on a highway fall between 93.18 and 118.

This means that 93.18 is one standard deviation below the mean and 118 is one standard deviation above the mean. That is, the difference between 118 and 93.18 is worth two standard deviations. So

`2s = 118 - 93.18`

`s = ((118 - 93.18))/(2)`

`s = 12.41`

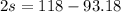
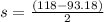
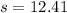
The approximate estimate of the standard deviation of the speeding ticket fines is of 12.41.