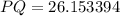Question

Please help me

I’ve been stuck on this question for hours, I need help and explanation please

Answer 1

`PQ=6√(19)`

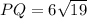
As a decimal:

`PQ\approx26.2`

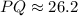
Explanation:

In a circle, the radius is the distance from the center of the circle to the circumference of the circle. In any given circle, the radius is the same, no matter what point on the circumference one measures it from.

In this case, (PO) is the radius with a measurement of (14). As one can see (RO) is also another radius, as (O) is the center of the circle, and (R) is a point on the circumference of the circle. Since (RO) and (PO) are both radii, one can say that (RO = PO = 14). Call the point where (RO) intersects (PQ) point (N). Therefore, one can form the following equation:

NO + NR = RO

Substitute,

NO + 9 = 14

Solve,

NO = 5

Since (NO) intersects (PQ) at a perpendicular angle, therefore triangle (PNO) is a right triangle. Therefore, one can use the Pythagorean theorem to find the unknown side length, (PN). The Pythagorean theorem states the following,

`a^2+b^2=c^2`

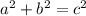
Where (a) and (b) are the sides of the triangle that are adjacent (next to) to the right angle and side (c) is the hypotenuse, the side opposite the right angle.

Substitute in the given sides and solve,

`a^2+b^2=c^2\\(PN)^2+5^2=14^2`

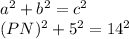
Simplify,

`(PN)^2+25=196\\`

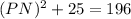
Inverse operations,

`(PN)^2=171`

`PN=√(171)\\PN=3√(19)`

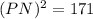
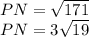
Multiply the value of (PN) by (2) to find the value of (PQ). This must be done since radius (RO) splits segment (PQ) in half at a right angle. Such a segment is often referred to as a perpendicular bisector.

`2(PN) = PQ\\\\2(3√(19))=PQ\\\\6√(19)=PQ`

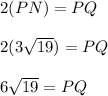
As a decimal:

`PQ=26.153394`

Answer 2

PQ = 26.2 cm

Explanation:

PQ is twice the length of the long leg of the triangle

It will take several steps to find it

----------------------------------------------

The short leg of the right triangle is 14 - 9 = 5 cm

Use the pythagorean theorem to find the long leg

a² + b² = c²

a² + 5² = 14²

a² + 25 = 196

a² = 171

a = 13.076696830622021

PQ = 2 * 13.076696830622021

PQ = 26.153393661244041

Rounded

PQ = 26.2 cm