Answer:
Explanation:
F(x) = x² - 2x + 1
= (x - 1)²
By comparing this equation with the vertex form of the quadratic equation,
y = (x - h)² + k
Here, (h, k) is the vertex
Vertex of the parabola → (1, 0)
x-intercepts → (x - 1)² = 0
x = 1
y-intercepts → y = (0 - 1)²
y = 1
Now we can draw the graph of the given function,
From this graph,
As x → 0,
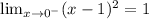
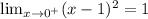
f(0) = (0 - 1)²
= 1
Since,
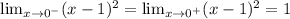
Therefore, given function is continuous at x = 0.