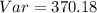Question

In a data distribution, the first quartile, the median and the means are 30.8, 48.5 and 42.0

respectively. If the coefficient skewness is , use the information to answer

questions 9 and 10.

9. What is the approximate value of the third quartile

(Q3 ), correct to 2 decimal places?

​

Answer 1

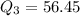`Q_3 = 56.45` --- The third quartile

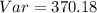`Var = 370.18` -- Variance

Explanation:

Given

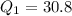`Q_1 = 30.8` -- First quartile

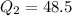`Q_2 = 48.5` --- Median

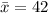`\bar x = 42` --- Mean

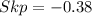`Skp = -0.38` --- Coefficient of skewness

Solving (9): The third quartile
`Q_3`

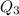
This is calculated from

`Skp = (Q_1 + Q_3 - 2Q_2)/(Q_3 - Q_1)`

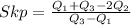
So, we have:

`-0.38 = (30.8 + Q_3- 2*48.5)/(Q_3 - 30.8)`

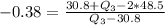
Cross Multiply

`-0.38 (Q_3 - 30.8)= 30.8 + Q_3- 2*48.5`

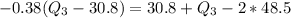
Open bracket

`-0.38Q_3 + 11.704= 30.8 + Q_3- 97.0`

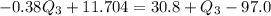
Collect like terms

`-0.38Q_3 -Q_3= 30.8 - 97.0- 11.704`

`-1.38Q_3= -77.904`

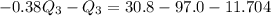
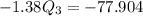
Divide both sides -1.38

`Q_3 = (-77.904)/(-1.38)`

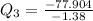
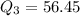`Q_3 = 56.45` --- approximated

Solving (b): The variance

First, calculate the standard deviation from:

`3IQR = 4SD`

`IQR= Q_3 - Q_1`

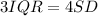
So:

`3IQR = 4SD`

`3(Q_3 - Q_1) = 4SD`

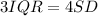
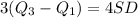
Make SD the subject

`SD = (3)/(4)(Q_3 - Q_1)`

`SD = (3)/(4)(56.45 - 30.8)`

`SD = (3)/(4)*25.65`

`SD = (3*25.65)/(4)`

`SD = (76.95)/(4)`

`SD = 19.24`

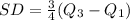
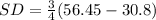
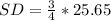
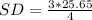
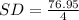
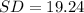
So, the variance is:

`Var = SD^2`

`Var = 19.24^2`

`Var = 370.18`