Question

An engine operates on a Carnot cycle that uses 1mole of an ideal gas as the

working substance and operates from a most compressed stage of 100 Nm and
327 K. It expands isothermally to a pressure of 90 Nm and then adiabatically to a
most expanded stage of 27 K. Calculate the AU, 9, and w for each step. Calculate
the net work done and the efficiency of the cycle [Cv,m for the gas) is 25 J/k/mol.​

Answer 1

Step 1;

q = w = -0.52571 kJ, ΔS = 0.876 J/K

Step 2

q = 0, w = ΔU = -7.5 kJ, ΔH = -5.00574 kJ

Step-by-step explanation:

The given parameters are;

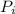`P_i` = 100 N·m

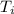`T_i` = 327 K

`P_f` = 90 N·m

Step 1

For isothermal expansion, we have;

ΔU = ΔH = 0

w = n·R·T·ln(
`P_f`/
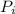`P_i`) = 1 × 8.314 × 600.15 × ln(90/100) = -525.71

w ≈ -0.52571 kJ

At state 1, q = w = -0.52571 kJ

ΔS = -n·R·ln(
`P_f`/
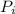`P_i`) = -1 × 8.314 × ln(90/100) ≈ 0.876

ΔS ≈ 0.876 J/K

Step 2

q = 0 for adiabatic process

ΔU = 25×(27 - 327) = -7,500

w = ΔU = -7.5 kJ

ΔH = ΔU + n·R·ΔT

ΔH = -7,500 + 8.3142 × 300 = -5,005.74

ΔH = ΔU = -5.00574 kJ