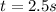Answer:
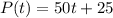
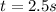
Step-by-step explanation:
Given
See attachment for graph
Solving (a): The graph equation.
Pick two points on the line of the graph
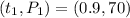
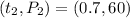
Calculate the slope (m)

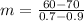
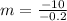
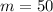
The equation is then calculated using:
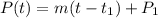

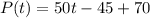
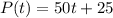
Solving (b): Solve for t when
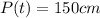
We have:
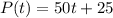
Substitute:
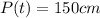
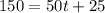
Collect like terms


Divide both sides by 50