Question

A small ship capable of making a speed of 6 knots through still water maintains a heading due east while being set to the south by an ocean current. The actual course of the boat is from A to B, a dis- tance of 10 nautical miles that requires exactly 2 hours. Determine the speed vC of the current and its direction measured clockwise from the north.

Answer 1

This question is incomplete, the missing diagram is uploaded along this answer below;

Answer:

the speed Vc of the current and its direction measured clockwise from the north is 0.71 m/s and 231.02° respectively

Step-by-step explanation:

Given the data in the question and as illustrated in the diagram below;

The absolute velocity of the ship Vs is 6 Knots due east

so we convert to meter per seconds

Vs = 6 Knots ×
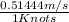`(0.51444 m/s)/(1 Knots)` = 3.0866 m/s

Next we determine the relative velocity of the ship Vs/c

Vs/c = AB / t

given that distance between A to B = 10 nautical miles which requires 2 hours

so we substitute

Vs/c = 10 nautical miles / 2 hrs

Vs/c = [10 nautical miles ×
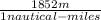`(1852 m)/(1 nautical-miles)` ] / [ 2 hrs ×
`(3600s)/(1hr)` ]

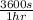Vs/c = 18520 / 7200

Vs/c = 2.572 m/s

Now, from the second diagram below, { showing the relative velocity polygon }

Now, using COSINE RULE, we calculate the velocity current.

Vc = √( V²s + V²s/c - 2VsSs/ccos10 )

we substitute

Vc = √( (3.0866)² + (2.572)² - (2 × 3.0866 × 2.572 × cos10 ) )

Vc = √( (3.0866)² + (2.572)² - (2 × 3.0866 × 2.572 × 0.9848 ) )

Vc = √( 9.527099 + 6.615184 - 15.6361 )

Vc = √0.506183

Vc = 0.71 m/s

Next, we use the SINE RULE to calculate the direction;

Vc/sin10 = Vs/c / sinθ

we substitute

0.71 / sin10 = 2.572 / sinθ

0.71 / 0.173648 = 2.572 / sinθ

4.0887 = 2.572 / sinθ

sinθ = 2.572 / 4.0887

sinθ = 0.62905

θ = sin⁻¹( 0.62905 )

θ = 38.98°

So, angle measured clock-wise will be;

θ = 270° - 38.98°

θ = 231.02°

Therefore, the speed Vc of the current and its direction measured clockwise from the north is 0.71 m/s and 231.02° respectively