Question

Problem 7.1 (10 points) Let pXnqn"0,1,... be a Markov chain with state space S " t1, 2, 3u and transition probability matrix P " ¨ ˝ 0.5 0.4 0.1 0.3 0.4 0.3 0.2 0.3 0.5 ˛ ‚. (a) Compute the stationary distribution π. (b) Is the stationary distribution π also the limiting distribution? Give a reason for your answer.

Answer 1

The responses to the given can be defined as follows:

Explanation:

For point a:

fixing probability vector that is
`W = [a b c]`

`\therefore`

relation:
`WT =W`

`\to 0.5a+0.3b+0.2c=a ..................(1)\\\\ \to 0.4a+0.4b+0.3c=b..............(2)\\\\ \to 0.1a+0.3b+0.5c=c.................(3)`

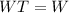
solving the value:

`a=0.3387 \\\\ b=0.3710\\\\ c=0.2903`

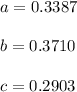
Therefore the stationary distribution
`\pi =[0.3387 \ 0.3710\ 0.2903]`

For point b:

`\pi` will be limiting distribution if
`\pi_j=\lin_(n\to \infity) (X_n=(j)/(X_0)=i) \Sigma_(√(j)) n_j=1`

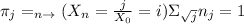
`\pi` satisfies the above condition so, it is limiting the distribution.