Question

Based on a random sample of 1140 adults, the mean amount of sleep per night is 7.96 hours. Assuming the population standard deviation for the amount of sleep per night is 1.6 hours, construct 95% confidence interval for the mean amount of sleep per night.

a. (7.67, 8.05)
b. (7.87, 8.05)
c. (8.09, 9.12)
d. (7.87, 8.23)

Answer 1

at 95% confidence interval, the mean amount of sleep per night is ( 7.87, 8.05 ).

Option b) (7.87, 8.05) is the correct answer.

Explanation:

Given the data in the question;

sample size n = 1140

sample mean x" = 7.96

standard deviation σ = 1.6

At 95% confidence interval,

significance level ∝ = 1 - 95% = 1 - 0.95 = 0.05

∝/2 = 0.05 / 2 = 0.025

Z-Critical
`Z_{\alpha /2` =
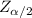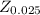`Z_{0.025` = 1.96

Top get the Margin of error E;

E =
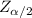`Z_{\alpha /2` × ( σ /√n )

we substitute

E = 1.96 × ( 1.6 /√1140 )

E = 0.09

So, At 95% confidence interval of the population mean is;

⇒ x" ± E

⇒ x" - E or x" + E

we substitute

⇒ 7.96 - 0.09, 7.96 + 0.09

⇒ 7.87, 8.05

Therefore, at 95% confidence interval, the mean amount of sleep per night is ( 7.87, 8.05 ).

Option b) (7.87, 8.05) is the correct answer.