GIVEN: The perimeter of triangle STU is 125.
The segments TW=21 cm
VW=30 cm
VT=24 cm
TO FIND: The length of the segment SU.
SOLUTION:
As corresponding sides must be same. so we have,
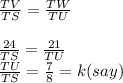
Then, TU=7k and TS=8k
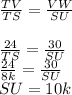
As the perimeter of triangle STU is 125.
so,
8·k+7·k+10·k=125
⇒25.k=125
⇒k=5
Therefore, SU=10×5=50