Answer:
a) The standard error for this estimate of the percentage of all young Americans who earned a high school diploma is 0.87%.
b) The margin of error, using a 95% confidence level, for estimating the percentage of all young Americans who earned a high school diploma is of 1.71%.
c) The 95% confidence interval for the percentage of all young Americans who earned a high school diploma is (85.29%, 88.71%).
d) The lower bound of the confidence interval is above 80%, which means that the confidence interval supports the claim that the percentage of young Americans who cam high school diplomas has increased.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
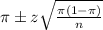
In which
z is the z-score that has a p-value of
 .
.
Standard error:
The standard error is:
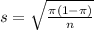
Margin of error:
The margin of error is:
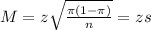
The confidence interval is:
Sample proportion plus/minus margin of error. So
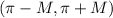
In a simple random sample of 1500 young Americans 1305 had earned a high school diploma.
This means that
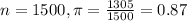
a. What is the standard error for this estimate of the percentage of all young Americans who earned a high school diploma?
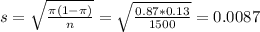
0.0087*100% = 0.87%.
The standard error for this estimate of the percentage of all young Americans who earned a high school diploma is 0.87%.
b. Find the margin of error, using a 95% confidence level, for estimating the percentage of all young Americans who earned a high school diploma.
95% confidence level
So
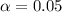 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
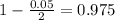 , so
, so
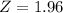 .
.
Then
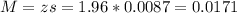
0.0171*100% = 1.71%
The margin of error, using a 95% confidence level, for estimating the percentage of all young Americans who earned a high school diploma is of 1.71%.
c. Report the 95% confidence interval for the percentage of all young Americans who earned a high school diploma.
87% - 1.71% = 85.29%
87% + 1.71% = 88.71%.
The 95% confidence interval for the percentage of all young Americans who earned a high school diploma is (85.29%, 88.71%).
d. Suppose that in the past, 80% of all young Americans earned high school diplomas. Does the confidence interval you found in part c support or refute the claim that the percentage of young Americans who cam high school diplomas has increased? Explain.
The lower bound of the confidence interval is above 80%, which means that the confidence interval supports the claim that the percentage of young Americans who cam high school diplomas has increased.