Question

Consider the function f (x) = StartFraction x squared + 11 x minus 12 Over x minus 1 EndFraction.

Which statement describes the discontinuity at x = 1?

a jump discontinuity that cannot be removed by extending the function

an infinite discontinuity that cannot be removed by extending the function

a removable discontinuity that can be removed by extending the function to include f(1) = 13

a removable discontinuity that can be removed by extending the function to include f(1) = –11


IT'S C!

Answer 1

C

Explanation:

I said so

Answer 2

"a removable discontinuity that can be removed by extending the function to include f(1) = 13"

Explanation:

We have the function:

`f(x) = (x^2 + 11*x - 12)/(x - 1)`

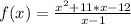
Here we have a problem when x = 1, because that makes the denominator to be equal to zero.

For now, let's see what happens to the numerator when x = 1

1^2 + 11*1 - 12 = 12 - 12 = 0

So x = 1 is a root of the numerator.

Let's find the other root of the numerator, here we can use Bhaskara's formula:

`x = (-11 \pm √(11^2 - 4*1*(-12)) )/(2*1) = (-11 \pm 13)/(2)`

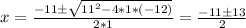
Then the two roots are:

x = (-11 + 13)/2 = 1

x = (-11 - 13)/2 = -12

And remember that a quadratic equation:

y = a*x^2 + b*x + c

With roots p and k, can be written as:

y = a*(x - p)*(x - k)

Then we can rewrite our numerator as:

1*(x - 1)*(x - (-12)) = (x - 1)*(x + 12)

Replacing that in the equation for f(x), we get:

`f(x) = (x^2 + 11*x - 12)/(x - 1) = ((x - 1)*(x + 12))/((x - 1)) = (x - 1)/(x -1) *(x + 12)`

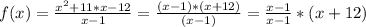
f(x) = x + 12

And, when evaluated in x = 1, we get:

f(1) = 1 + 12 = 13

Then the correct option is:

"a removable discontinuity that can be removed by extending the function to include f(1) = 13"