Question

A carousel moves in a counterclockwise direction. It makes one complete revolution every 16 seconds. Han is sitting 11 feet from the center of the carousel. Here is a view of the carousel from above. Based on the view from above, write an equation describing Han’s vertical position v, in feet, relative to the center of the carousel t seconds after the carousel starts moving.(Question 7)

Answer 1

`The \ vertica \ position \ of \ the \ carousel,\ v = 11 * sin \left ((\pi)/(2) * \left ((t)/(4) -1\right)\right )`

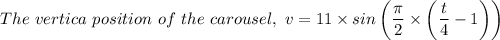
Explanation:

The parameters of the motion on the carousel are;

The time it takes the carousel to make one complete revolution, T = 16 seconds

The distance Han is sitting from the center = 11 feet

The motion of the carousel can be given by the equation of sinusoidal motion as follows;

v = a·sin(ω·t + c)

Where;

a = The amplitude of the sinusoidal motion = Han's distance from the center = 11 feet

ω = The angular velocity

t = Han's time in motion =

ω = 2·π/T = 2·π/16 rad/s

c = The phase shift

v = The vertical position of the carousel

Given that at the starting point when t = 0, y = minimum, therefore, sin(ω·t + c) = sin(ω×0 + c) = sin(c) = minimum = -1

c = arcsin(-1) = -π/2 we have

Therefore, when time after the carousel starts moving = t second, we have;

The vertical position of the carousel in feet, v = 11·sin((π/8)·t) - π/2) = 11×sin((π/2)·(t/4 - 1))