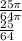Question

Find the probability that a randomly placed point falls within the smaller, inner circle.

The unshaded portion has a radius of 5 centimeters. The shaded path has a width of 8 centimeters.


5/8

25/169

64/78.5

15/24

Answer 1

The probability that a randomly placed point falls within the smaller, inner circle is 25/64

Explanation:

The remaining part of question is attached

Solution

The area of smaller circle is

`\pi r^2 = 25 \pi`

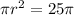
The area of large circle is

`\pi r^2 = 64 \pi`

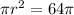
Area of the shaded region

Area of large circle - area of small circle

`64\pi -25\pi = 39\pi`

Probability that the point falls in the region of smaller circle is

`(25\pi )/(64\pi ) \\(25)/(64)`