Question

You drive past a potential parking space in center city. Your new car is travelling at 85% the speed of light. If your car is 6.0 m long (which you measured the day you bought it) and you observe the space to be 3.0 m, should you try to park? Why is your friend on the sidewalk (who hasn't studied relativity) so sure that you can park? How does the situation appear to him?

Answer 1

We should not try to park the car because its rest length is greater than the space available.

The car seems to be approximately equal to the friend (L = 3.16 m). Due to this reason he is sure to park.

Step-by-step explanation:

We should not try to park the car because its rest length is greater than the space available.

The friend is sure about parking because the car appears short in length to him. For this, we will solve Einstein's length contraction formula from theory of relativity:

`L = L_o\sqrt{1-(v^2)/(c^2)}`

where,

L = Relative length observed by friend = ?

L₀ = rest length = 6 m

v = relative speed = 85% of speed of light = 0.85c

Therefore,

`L = (6\ m)\sqrt{1-((0.85c)^2)/(c^2)}`

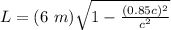
L = 3.16 m

Hence, the car seems to be approximately equal to the friend. Due to this reason he is sure to park.