Question

Demuestre que la función de onda: y(x, t) = A e^−i(kx−ωt+φ) satisface la ecuación de onda lineal. (donde i =√−1).

Answer 1

La ecuación de onda lineal para una función f(x, t) se escribe como:

`(d^2f)/(dt^2) = c^2*(d^2f)/(dx^2)`

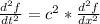
Donde c es una constante que depende de la velocidad de propagación de la onda.

En este caso, tenemos:

`f(x) = A*e^(-i*(k*x - w*t + \phi))`

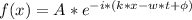
Recordar que la derivada de la exponente es tal que:

`k(x,y) = A*e^(c*x + n*y)\\dk/dx = c*A*e^(c*x + n*y)`

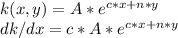
Entonces las derivadas de f van a ser:

`(df)/(dt) = (i*w)*f(x)`

`(d^2f)/(dt^2) = (i*w)^2*f(x) = -(w)^2*f(x)`

`(df)/(dx) = (-i*k)*f(x)`

`(d^2f)/(dx^2) = (-i*k)^2*f(x) = -k^2*f(x)`

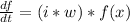
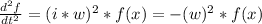
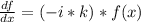
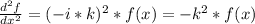
Entonces podemos reescribir la ecuación de onda como:

`(d^2f)/(dt^2) = c^2*(d^2f)/(dx^2)`

`-(w)^2*f(x) = c^2*(-k^2*f(x))`

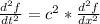
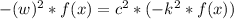
Ahora podemos simplemente definir c^2 = (w/k)^2 y vemos que la ecuación de onda se cumple.