I need answer Immediately pls!!!!!!

Question

asked Nov 21, 2022 141k views

1 Answer

AndrewGrant · Answer 1 · 2022-11-25T22:24:48+0000

Given:

Total number of students = 27

Students who play basketball = 7

Student who play baseball = 18

Students who play neither sports = 7

To find:

The probability the student chosen at randomly from the class plays both basketball and base ball.

Solution:

Let the following events,

A : Student plays basketball

B : Student plays baseball

U : Union set or all students.

Then according to given information,

n(U)=27

n(A)=7

n(B)=18

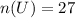
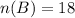
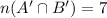
$n(A'\cap B')=7$

We know that,

$n(A\cup B)=n(U)-n(A'\cap B')$

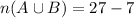
$n(A\cup B)=27-7$

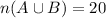
$n(A\cup B)=20$

Now,

$n(A\cup B)=n(A)+n(B)-n(A\cap B)$

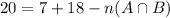
$20=7+18-n(A\cap B)$

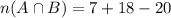
$n(A\cap B)=7+18-20$

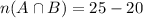
$n(A\cap B)=25-20$

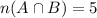
$n(A\cap B)=5$

It means, the number of students who play both sports is 5.

The probability the student chosen at randomly from the class plays both basketball and base ball is

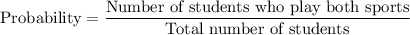
$\text{Probability}=\frac{\text{Number of students who play both sports}}{\text{Total number of students}}$

$\text{Probability}=(5)/(27)$

Therefore, the required probability is
.
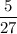