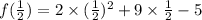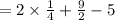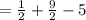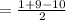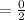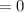Answer:
-5 ; 1/2
Explanation:
GIVEN :-
- A quadratic polynomial f(x) = 2x² + 9x - 5
TO FIND :-
- Zeroes of f(x) = 2x² + 9x - 5
GENERAL CONCEPTS TO BE USED IN THIS QUESTION :-
Lets say there's a quadratic polynomial f(x) = ax² + bx + c , whose factors are (x - α) & (x - β). To find the values of x for which f(x) will be zero , equate the factors of f(x) with 0.
⇒ (x - α) = 0 & (x - β) = 0
⇒ x = α & x = β
Hence, it can be concluded that if (x - α) & (x - β) are factors of f(x) , then α & β are the roots of f(x).
SOLUTION :-
Factorise f(x) = 2x² + 9x - 5.
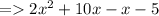
- Take '2x' common from first two terms & '-1' from last two terms.
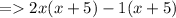
- Take (x + 5) common from the whole expression.
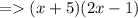
So , the factors of f(x) are (x + 5) & (2x - 1). Now equate the factors with zero.
⇒ (x + 5) = 0 & (2x - 1) = 0
⇒ x = -5 & x = 1/2
∴ The zeroes of f(x) = 2x² + 9x - 5 are (-5) & (1/2)
VERIFICATION :-
1) Put x = -5 in f(x) = 2x² + 9x - 5
⇒ f(-5) = 2(-5)² + 9×(-5) - 5
= 50 - 45 - 5
= 50 - 50
= 0
2) Put x = 1/2 in f(x) = 2x² + 9x - 5