Question

Help plz..And No links!! I repeat No links!!

Answer 1

Given:

ST || RU

To find:

The measure of QS.

Solution:

In triangle QRU and QST,

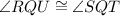`\angle RQU\cong \angle SQT` [Common angle]

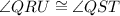`\angle QRU\cong \angle QST` [Corresponding angle]

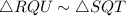`\triangle RQU\sim \triangle SQT` [AA property of similarity]

The corresponding sides of similar triangles are proportional.

`(QR)/(QS)=(QU)/(QT)`

`(23)/(QS)=(25)/(25+50)`

`(23)/(QS)=(25)/(75)`

`(23)/(QS)=(1)/(3)`

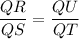
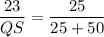
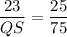
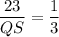
On cross multiplication, we get

`3(23)=1(QS)`

`69=QS`

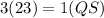
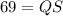
Therefore, the measure of QS is 69.