Answer:
Explanation:
Arc length of a circle is given by,
Arc length =
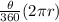
Here, θ = Central angle subtended by the arc
r = Radius of the circle
From the given picture,
θ = 45°
r = 1 unit
Therefore, arc length =
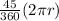
=

=
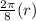
=
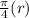
Arc length =
 units
units
=
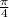 units
units
Angle θ has a measure =
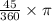
=
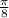 radians
radians