Answer:

Step-by-step explanation:
This question asks us to convert liters to moles. We know that 1 mole of any gas contains 22.4 liters. This includes ammonia (NH₃), so let's set up a ratio.
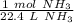
Since we are converting 95.5 liters of ammonia to moles, we multiply by that value.
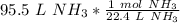
The units of liters of ammonia (L NH₃) cancel.
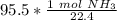
Condense into 1 fraction.
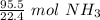
Divide.
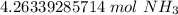
The original measurement of liters (95.5) has 3 significant figures. Our answer must have the same. For the number we calculated, that is the hundredth place.
The 3 in the thousandth place (4.26339285714) tells us to leave the 6 in the hundredth place.
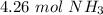
95.5 liters of ammonia is equal to 4.26 moles of ammonia.