Answer:
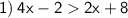
Add 2 from both sides:
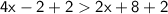
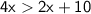
Subtract 2x from both sides:
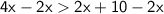
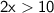
Divide both sides by 2:
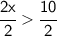

_______________________________
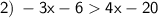
Add 6 from both sides:
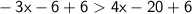
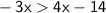
Subtract 4x from both sides:
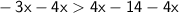
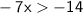
Multiply both sides by -1:
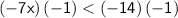
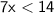
Divide both sides by 7:
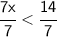

_______________________________
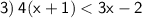
Apply distributive property:
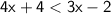
Subtract 4 from both sides:
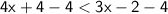
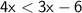
Subtract 3x from both sides:
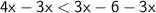

_______________________________
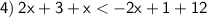
Combine like terms:
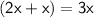
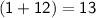
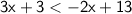
Subtract 3 from both sides:
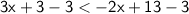
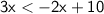
Add 2x from both sides:
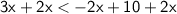
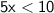
Divide both sides by 5:
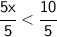

________________________________
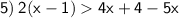
Combine like terms:
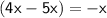
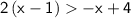
Apply distributive property:

Add 2 from both sides:
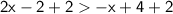
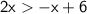
Add x from both sides:
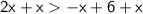
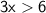
Divide both sides by 3:
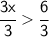

_______________________________
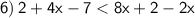
Subtract 2 from both sides:
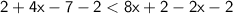
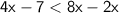
Combine like terms:
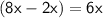
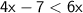
Add 7 from both sides:
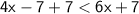
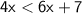
Subtract 6x from both sides:
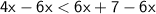
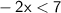
Multiply both sides by -1:
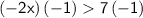
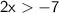
Divide both sides by 2:
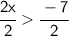
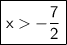
_______________________________________