Answer:
a) Length of the arc:
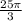
 or ≈ 26.18
or ≈ 26.18

b) Area of the sector:
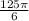
 or ≈ 65.45
or ≈ 65.45
c) 16
 rad or 2880°
rad or 2880°
Explanation:
If a is the length of the arc, r is the radius of the sector and 0 the central angle in radians.
Use the formula:
[set r = 5 m, 0 =
 (given)]
(given)]
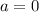 ·
·

⇒
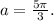

⇒
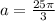 ≈
≈
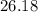

The arc length of the watered sector is
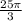
 or ≈ 26.18.
or ≈ 26.18.
----------------------------------------------------------------------------------------------
Recall, the area A of a circle (obviously
 ) with a radius
) with a radius
 is given by the formula:
is given by the formula:
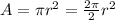
So the area of the circular sector with radius r and central 0 (in radians) will be:
[set r = 5m , 0 =
 (given)]
(given)]
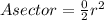
⇒
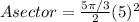
⇒
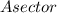 =
=
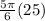
⇒
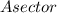 =
=
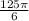 ≈ 65.45
≈ 65.45
The area of the watered sector is
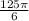
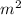 or ≈ 65.45
or ≈ 65.45
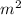 .
.
-----------------------------------------------------------------------------------------------
From the given information we know that the sprinkler perform a full revolution (2
 rad) every 15 sec so we will make the following proportion:
rad) every 15 sec so we will make the following proportion:
 =
=
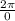
⇒
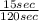 =
=
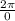
⇒ 0 =
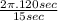
⇒ 0 =
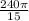
⇒ 0 =

We can convert the angle of 0 =
 rad to degrees as shown:
rad to degrees as shown:
 = 16
= 16
 ×
×
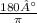
⇒
 = 2880°
= 2880°
Finally the sprinkler rotates 16
 rad or 2880° in 2 minutes.
rad or 2880° in 2 minutes.