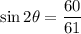Question

If tanΘ = 6/5 and cosΘ < 0, what is sin2Θ?

An explanation on how to solve this problem would be great, thanks!!

Answer 1

`\displaystyle \sin2\theta=(60)/(61)`

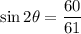
Explanation:

We are given that:

`\displaystyle \tan\theta=(6)/(5)\text{ and } \cos\theta <0`

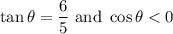
And we want to find the value of sin(2θ).

First, recall that tangent is the ratio of the opposite side to the adjacent side.

Therefore, the hypotenuse is:

`h=√(6^2+5^2)=√(61)`

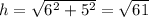
Next, note that tangent is positive and cosine is negative. Tangent is positive in QI and QIII. Cosine is negative in QII and QIII.

Hence, we can conclude that θ must be in QIII.

In QIII, sine is negative, cosine is negative, and tangent is positive.

And with respect to θ, our opposite side is 6, adjacent side is 5, and the hypotenuse is √(61).

We can rewrite our expression as:

`\sin2\theta=2\sin\theta\cos\theta`

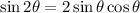
Using the above information, substitute:

`\displaystyle =2\left(-(6)/(√(61))\right)\left(-(5)/(√(61))\right)`

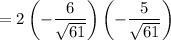
Simplify. Hence:

`\displaystyle \sin2\theta=(60)/(61)`