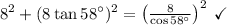Question

Someone pls help, its on trig ratios.

Answer 1

`BC=12.8,\\AC=15.1`

Explanation:

In right triangles only, the tangent of an angle is equal to its opposite side divided by its adjacent side.

Therefore, we have the following equation:

`\tan 58^(\circ)=(BC)/(8)`

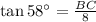
Solving, we get:

`BC=8\tan 58^(\circ)\approx \boxed{12.8}`

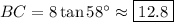
Also in right triangles only, the cosine of an angle is equal to its adjacent side divided by the hypotenuse of the triangle.

`\cos 58^(\circ)=(8)/(AC),\\AC=(8)/(\cos 58^(\circ)),\\AC\approx \boxed{15.1}`

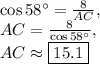
We can also use the Pythagorean theorem now that we've found BC. However, if you choose to do so, make sure you don't use a rounded value for BC, as that could cause a notable deviation in your final answer.

Using the Pythagorean theorem to verify our answers:

`8^2+(8\tan 58^(\circ))^2=\left((8)/(\cos 58^(\circ))\right)^2\:\checkmark`