Answer:
Explanation:
To find the vertex, we need to put this into vertex form, which is done by completing the square on the quadratic. Begin by moving the 8 over to he other side of the equals sign:
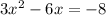
Now factor out the 3:

Now take half the linear term, square it, and add it to both sides. Our linear term is 2. Half of 2 is 1, and 1 squared is 1:

We added a 3 on the right because 3 times the 1 we added in is 3. Cleaning that up a bit gives us the perfect square binomial on the left and -5 on the right:
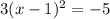
and when we move the -5 back over by adding we have
 and our vertex is seen to be (1, 5)
and our vertex is seen to be (1, 5)