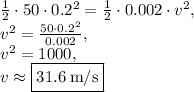Question

We have a toy gun with a spring constant of 50 N/m. The spring is compressed by 0.2 m. If you neglect friction and the mass of the spring, at what speed will a 2 g projectile be ejected from the gun

Answer 1

`31.6\:\mathrm{m/s}`

Step-by-step explanation:

The elastic potential energy of a spring is given by
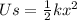`Us=(1)/(2)kx^2`, where
`k` is the spring constant of the spring and
`x` is displacement from point of equilibrium.

When released, this potential energy will be converted into kinetic energy. Kinetic energy is given by
`KE=(1)/(2)mv^2`, where
`m` is the mass of the object and
`v` is the object's velocity.

Thus, we have:

`Us=KE,\\(1)/(2)kx^2=(1)/(2)mv^2`

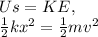
Substituting given values, we get:

`(1)/(2)\cdot 50\cdot 0.2^2=(1)/(2)\cdot 0.002\cdot v^2,\\v^2=(50\cdot 0.2^2)/(0.002),\\v^2=1000,\\v\approx \boxed{31.6\:\mathrm{m/s}}`