Question

A 13-foot ladder is leaning against a building, forming a right triangle. The height where the ladder touches the building is 7 feet more than the distance of the base of the ladder from the building. At what height does the ladder hit the building

Answer 1

Explanation:

The length of the ladder is the length of the hypotenuse of the right triangle formed. Since the height up the building is based on the distance the ladder is from the base of the building, and that distance is x, then the height up the building is x + 7. So what we have is a right triangle with one leg measuring x, the other leg measuring x + 7, and the hypotenuse measuring 13. Set up using Pythagorean's Theorem:

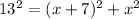`13^2=(x+7)^2+x^2` and do some simplifying. The left side is easy since 13-squared is 169; the right side not so much. We first have to expand that set of parenthesis by multiplying x + 7 by itself twice to get a second degree polynomial:

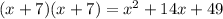`(x+7)(x+7)=x^2+14x+49` and now we have:

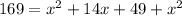`169=x^2+14x+49+x^2` which simplifies down a bit to

`169=2x^2+14x+49`

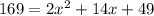
The only way to solve this for x, the height up the side of the building, is to factor. In order to do that, everything has to be on one side of the equals sign, setting the whole messy thing equal to 0:

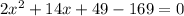`2x^2+14x+49-169=0` and

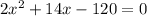`2x^2+14x-120=0`. Begin by factoring out a 2:

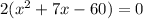`2(x^2+7x-60)=0` and then factor the remaining quadratic using whatever method you are currently using in class to solve for x. Doing this will give that

x = -12 and 5. Since a side length will never be negative, we determine that x = 5 which is the distance between the bases of the buildings, and the height up the building where the ladder hits it is 12.