Answer:
Step-by-step explanation:
The angle here makes this a very interesting problem. We will use only the y-dimension information since we are given nothing pertinent in the x-dimension. Nothing there is useful to solving this problem. We are given (and know from experience) the following:
θ = 35.8°
v₀ = 26.2 m/s
Δx = -46.4 m
a = -9.8 m/s/s
t = ???
Time is our main unknown. The displacement is negative because, in the end, the small object will end up BELOW the point from which it is launched. That's important!!
Another thing we need to understand is that the velocity we are given is a "blanket" velocity; it is neither the upwards velocity nor the horizontal velocity. That's for us to find out using either cos or sin. In the y-dimension, we use the sin identity to find the upwards velocity (which is VERY different from the horizontal velocity {unless we are dealing with a 45 degree angle where sin and cos are the same}). So first we need to find the initial velocity in this dimension specifically:
26.2sin35.8 = 15.3 m/s
That's the initial velocity we will use in the problem now. The equation for this is:
Δx = v₀t +
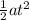 and filling in the given info:
and filling in the given info:
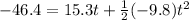 It looks like this will have to be factored if we are going to solve for t. Get everything on one side and factor the resulting quadratic:
It looks like this will have to be factored if we are going to solve for t. Get everything on one side and factor the resulting quadratic:
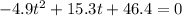 and factoring that gives you 2 values for t:
and factoring that gives you 2 values for t:
t = -1.9 sec and t = 5.0 sec
Since we all know that time can NEVER be negative, t = 5.0 sec.