Question

Convert the equation into standard form 25x^2 -9y^2+200x +18y +166=0

Answer 1

Explanation:

You'd have to be really familiar with conic sections to know what to do with this. Good thing I am! ; )

Begin by grouping the x terms together and the y terms together, and getting the constant on the other side of the equals sign:

`25x^2+200x-9y^2+18y=-166`

Now we need to complete the square on the x terms and the y terms. Do this by first factoring out the leading coefficient from each, the 25 from the x's and the 9 from the y's:

`25(x^2+8x)-9(y^2+2y)=-166`

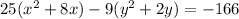
Now take half the linear term in each set of parenthesis, square it, and add it in to both sides, remembering the multiplier outside (the 25 and the 9). Our x linear term is 8. Half of 8 is 4, and 4 squared is 16, so we add a 16 into the parenthesis with the x's; our y linear term is 2. Half of 2 is 1 and 1 squared is 1, so we add a 1 into the parenthesis with the y's:

`25(x^2+8x+16)-9(y^2+2y+1)=-166+400-9`

Note the 400 and -9 on the right side now. 25 times 16 is 400; we didn't just add in a 16, we have to multiply the scalar number into it before we know what we REALLY added in. And the -9 comes from multiplying the -9 times 1.

The reason we do this is to get the perfect square binomials on the left that we created while completing the square:

`25(x+4)^2-9(y+1)^2=225`

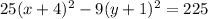
Now, finally we will divide both sides by 225 to get this conic into standard form:

`((x+4)^2)/(9) -((y+1)^2)/(25) =1`

This is a hyperbola with a horizontal transverse axis and a center of (-4, -1). The reason we know it's not an ellipse is because an ellipse will always have a + sign separating the x-squared from the y-squared whereas a hyperbola always has a - sign separating them. And we also know it's not a circle because the values of the leading coefficients weren't the same.