Answer:
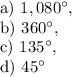
Explanation:
a) The sum of the interior angles of a polygon with
 sides is equal to
sides is equal to
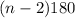 . Since an octagon has 8 sides, substitute in
. Since an octagon has 8 sides, substitute in
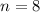 :
:

b) The sum of the exterior angles for any polygon is equal to
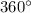 .
.
c) By definition, all regular shapes have equal angles and sides. Since we've found the total sum of the interior angles of an octagon in part a, each interior angle of a regular octagon must be
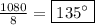
d) Similar to part c, all regular shapes must have equal angles and sides. From part b, we know the sum of the exterior angles of a octagon is
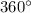 , thus we have
, thus we have
