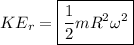Question

A disk of Radius R with a uniform distibution of mass"m" rotater about an axis perpendicular to its place at the rim with angular speed "w" the moment of Inertia of the disc about an axis through the contre MR² What is the KE of the disk?​

Answer 1

`(1)/(2)mR^2\omega^2`

Step-by-step explanation:

The rotational kinetic energy of an object is given by
`KE_r=(1)/(2)I\omega^2`, where
`I` is the object's moment of inertia/rotational inertia and
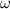`\omega` is the object's angular speed.

What we're given:

• The object's moment of inertia:
  `I=MR^2`
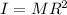
• The object's radius, mass, and angular speed:
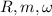  `R, m, \omega`, respectively

Since no numerical value is given for any of these, it is implied the desired answer will be an equation in terms of the variables given.

Substituting
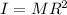`I=MR^2`:

`KE_r=\boxed{(1)/(2)mR^2\omega^2}`