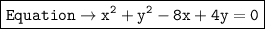We need to determine the equation of the circle graphed in the attachment. Firstly we know the Standard equation of a Circle as ,
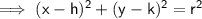
- Where ( h , k ) is centre and r is radius.
Let's find out the radius . As ,
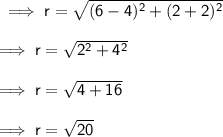
Substituting the respective values :-
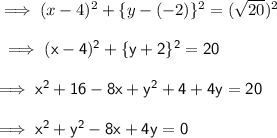
Answer :-