Explanation:
By question , it's given that the X intercept is (5,0) and the y intercept is (0,8) . And we need to find the y-intercept of the graph of f(x) + 3 . For that , firstly let's find out the equation of the line.
- We can use here two point form of the line .So that , the equation would be ,

Let us say that this is f(x) :-
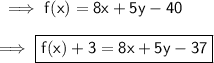
Plot its graph :-
We can either convert it into intercept form but plotting a graph can also be done to find y intercept .

Refer to attachment for graph .
Hence the y Intercept is 7.4 .