Question

Members from 6 different school organizations decorated floats for the homecoming parade. How many different ways can first, second, and third prize be awarded?

Answer 1

Answer: 120 different ways

=======================================================

Step-by-step explanation:

There are...

• 6 ways to select the first place winner
• 5 ways to pick the second place winner
• 4 ways to pick the third place winner

We start with 6, and count down by 1 each time we fill up a slot. We stop once the third slot is filled or accounted for. The countdown is to ensure that we don't pick the same person twice. From here, multiply those values: 6*5*4 = 30*4 = 120

Interestingly, this is equal to 5! = 5*4*3*2*1 = 120 because the 3*2 becomes 6 and that *1 at the end doesn't affect things. Though usually results of permutation problems don't always end up like this. The order matters because a result like ABC is different from BAC, where A,B,C,D,E,F are the six school organizations.

As a slightly longer way to do the problem, you can use the nPr formula which is
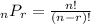`_nP_r = (n!)/((n-r)!)` where n = 6 and r = 3 in this case. The exclamation marks indicate factorial. If you go this route, you should find that one of the steps will involve 6*5*4.