Question

Complete the assignment on a separate sheet of paper

Please attach pictures of your work.

Answer 1

TO FIND :-

• Length of all missing sides.

FORMULAES TO KNOW BEFORE SOLVING :-

• 
  `\sin \theta = (Side \: opposite \: to \: \theta)/(Hypotenuse)`
• 
  `\cos \theta = (Side \: adjacent \: to \: \theta)/(Hypotenuse)`
• 
  `\tan \theta = (Side \: opposite \: to \: \theta)/(Side \: adjacent \: to \: \theta)`

SOLUTION :-

1) θ = 16°

Length of side opposite to θ = 7

Hypotenuse = x

`=> \sin 16 = (7)/(x)`

`=> (7)/(x) = 0.27563......`

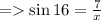
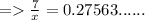
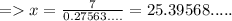`=> x = (7)/(0.27563....) = 25.39568.....` ≈ 25.3

2) θ = 29°

Length of side opposite to θ = 6

Hypotenuse = x

`=> \sin 29 = (6)/(x)`

`=> (6)/(x) = 0.48480......`

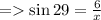
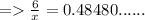
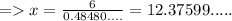`=> x = (6)/(0.48480....) = 12.37599.....` ≈ 12.3

3) θ = 30°

Length of side opposite to θ = x

Hypotenuse = 11

`=> \sin 30 = (x)/(11)`

`=> (x)/(11) = 0.5`

`=> x = 0.5 * 11 = 5.5`

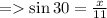
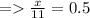
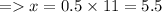
4) θ = 43°

Length of side adjacent to θ = x

Hypotenuse = 12

`=> \cos 43 = (x)/(12)`

`=> (x)/(12) = 0.73135......`

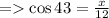
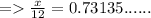
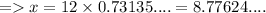`=> x = 12 * 0.73135.... = 8.77624....` ≈ 8.8

5) θ = 55°

Length of side adjacent to θ = x

Hypotenuse = 6

`=> \cos 55 = (x)/(6)`

`=> (x)/(6) = 0.57357......`

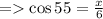
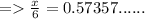
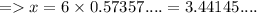`=> x = 6 * 0.57357.... = 3.44145....` ≈ 3.4

6) θ = 73°

Length of side adjacent to θ = 8

Hypotenuse = x

`=> \cos 73 = (8)/(x)`

`=> (8)/(x) = 0.29237......`

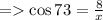
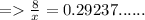
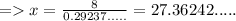`=> x = (8)/(0.29237.....) = 27.36242.....` ≈ 27.3

7) θ = 69°

Length of side opposite to θ = 12

Length of side adjacent to θ = x

`=> \tan 69 = (12)/(x)`

`=> (12)/(x) = 2.60508......`

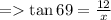
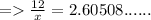
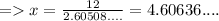`=> x = (12)/(2.60508....) = 4.60636....` ≈ 4.6

8) θ = 20°

Length of side opposite to θ = 11

Length of side adjacent to θ = x

`=> \tan 20 = (11)/(x)`

`=> (11)/(x) = 0.36397......`

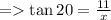
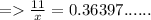
`=> x = (11)/(0.36397....) =30.22225....` ≈ 30.2