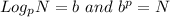Could someone please help me?

Question

asked Jan 24, 2022 221k views

1 Answer

Alptugay · Answer 1 · 2022-01-30T23:30:14+0000

Answer:

A.
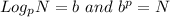
$Log_p N = b \ and \ b^p = N$

Explanation:

A. The given options are;

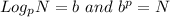
$Log_p N = b \ and \ b^p = N$

For
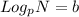Log_p N = b we have;

p^b = N

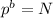
However;

b^p = N

Where, p ≠ b

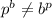
$p^b \\eq b^p$

Therefore;

N ≠ N for the given pair and the pair are therefore, not equivalent

B. x = √y and
x = y^(1/2)

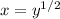
We note that

x = √y =
y^(1/2)

We have;

x =
y^(1/2) , by transitive property

Therefore, the pair, x = √y and
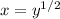x = y^(1/2) are equivalent

C.
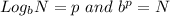
$Log_b N = p \ and \ b^p = N$

From
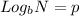Log_b N = p , we have;

b^p = N

Therefore,
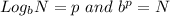$Log_b N = p \ and \ b^p = N$ are equivalent pairs as
b^p = N can be obtained from

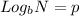
D. ㏑x = y and x =
e^y

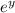
$ln \ x = ln_e \ x = y$ , therefore, by rules of logarithm, we have;

x =
e^y

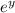
Therefore, ㏑x = y and x =
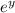e^y are equivalent pairs, as x =
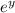e^y can be obtained from ln x.

Therefore;

The option which are not equivalent pair is option is
$Log_p N = b \ and \ b^p = N$