Question

the operation * is defined on the set R of all real number by 2a +3b ÷ a +b evaluate 2*(3*4)​

Answer 1

9514 1404 393

Answer:

2*(3*4) = 41/16

Explanation:

Your function is not carefully defined.* We assume you intend ...

f(a, b) = (2a +3b)/(a +b)

and you want to find ...

f(2, f(3, 4))

__

Filling in the values and doing the arithmetic, we have ...

`2*(3*4)=(2\cdot2+3\cdot(2\cdot3+3\cdot4)/(3+4))/(2+(2\cdot3+3\cdot4)/(3+4))=(4+3\cdot(18)/(7))/(2+(18)/(7))\\\\=(4\cdot7+3\cdot18)/(2\cdot7+18)=(82)/(32)=\boxed{(41)/(16)}`

_____

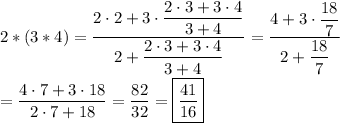
* We have assumed that the definition is describing the result of using the infix operator * in an expression of the form a*b. We have also assumed that your use of the ÷ symbol means ...

a*b ≡ (2a+3b)/(a+b)

as opposed to the strict Order of Operations interpretation ...

a*b ≡ 2a + (3b/a) +b