Question

Find the measure of the are or angle indicated. Assume that lines which appear tanget are tangents​

Answer 1

Given:

In a circle, two chords CE and DU intersect each other inside the circle at B.

Measure of arc CD = 185 degrees.

Measure of arc EU = 55 degrees.

To find:

The measure of angle CBD.

Solution:

Intersecting chords theorem: According to this theorem, if two chords intersect each other inside the circle then the measure of angle on the intersection is half of the sum of intercepted arcs.

Using Intersecting chords theorem, we get

`m\angle CBD =(1)/(2)(arcCD+arcEU)`

`m\angle CBD =(1)/(2)(185^\circ +55^\circ )`

`m\angle CBD =(1)/(2)(240^\circ )`

`m\angle CBD =120^\circ`

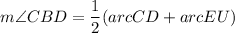
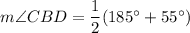
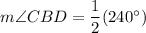
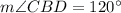
Therefore, the measure of angle CBD is 120 degrees.